STAT 301 Lab

Lab 6: Statistical Inference

T.A.: Yixuan Qiu

Confidence Interval

• Example: estimate population mean $\mu$
• The sample mean $\bar{X}$, a single number, is usually not enough nor reliable.
• Instead, we use an interval of the form $$estimate \pm margin\ of\ error$$ to "capture" the true mean.

C.I. for $\mu$

• If we know the population standard deviation $\sigma$, then the confidence interval for $\mu$ is $$\left(\bar{X}-z^*\frac{\sigma}{\sqrt{n}}, \bar{X}+z^*\frac{\sigma}{\sqrt{n}}\right)$$
• The bottom of the t-table gives the value of $z^*$ corresponding to different confidence level $C$
  • $C=90\%\Rightarrow z^*=1.645$
  • $C=95\%\Rightarrow z^*=1.960$
  • $C=99\%\Rightarrow z^*=2.576$

Hypothesis Testing

• Draw conclusion on a statement about the population
• Steps
  • State null hypothesis and alternative hypothesis
  • Calculate test statistic
  • Find P-value
  • Make conclusion

State Hypotheses

• Want to test whether the populatoin mean $\mu$ is greater than $\mu_0$ or not $$H_0:\mu=\mu_0\quad H_a:\mu>\mu_0$$
• Want to test whether the populatoin mean $\mu$ is less than $\mu_0$ or not $$H_0:\mu=\mu_0\quad H_a:\mu<\mu_0$$
• Want to test whether the populatoin mean $\mu$ is equal to $\mu_0$ or not $$H_0:\mu=\mu_0\quad H_a:\mu\neq\mu_0$$

Test Statistic

• If population standard deviation $\sigma$ is given, we calculate the z-score for $\bar{X}$ $$z=\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$$

P-value

• $H_a:\mu>\mu_0$ $$P-value = P(Z>z)$$
• $H_a:\mu<\mu_0$ $$P-value = P(Z<z)$$
• $H_a:\mu\neq\mu_0$ $$P-value = 2[1-P(Z<|z|)]$$

Conclusion

• If P-value < $\alpha$, we reject the null hypothesis
• If P-value > $\alpha$, we do not reject the null hypothesis
• We NEVER say "accept"

Moving to t Test

• When $\sigma$ is UNKNOWN, we use t test instead
• Use SPSS to do this
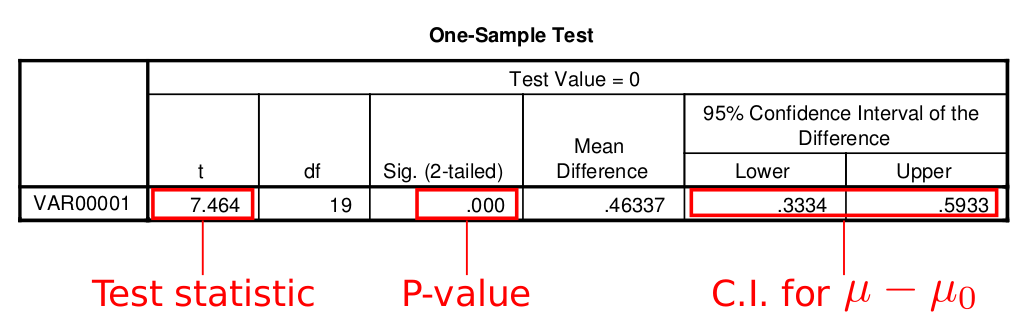
  • SPSS will give you P-value for two-sided test
  • P-value for one-sided test = 0.5 * P-value for two-sided test
  • The confidence interval that SPSS gives you is about $\mu-\mu_0$, not $\mu$, so you should add $\mu_0$ to both limits of the interval

Moving to t Test

Robustness Guidelines

• When is t test appropriate?
• If $n<15$, data should be Normally distributed with no outliers or skewness
• If $15\le n < 40$, data should be fairly symmetric, Normally distributed with no outliers or heavy skewness
• If $n\ge 40$, as long as no outliers