STAT 301 Lab

Lab 5: Normal Distribution

T.A.: Yixuan Qiu

Probability Statement

• We have some quantity $X$ that is a random variable
• $P(X>60)$ reads as "the probability that $X$ is greater than 60"
• You also need to know how to transform statements back to mathematical formulas

Normal Distribution

• Normal distribution helps us to calculate those probabilities
• It has a bell-shaped, symmetric, unimodal density curve
• A Normal distribution with mean $\mu$ and standard deviation $\sigma$ is usually denote by $N(\mu, \sigma^2)$

Typical Problems

• You are give that some quantity $X$ that follows a normal distribution with mean $\mu$ and standard deviation $\sigma$
• $\mu$ and $\sigma$ are given in concrete numbers
• Calculate
  • $P(X<x_0)$ for some number $x_0$
  • $P(X>x_0)$
  • Find $x_0$ such that it is in the top $\alpha$% of the population

$P(X<x_0)$

• Calculate $z$-score $$z=\frac{x_0-\mu}{\sigma}$$
• Look into the Normal Table

Example

• Find the probability if $z=0.95$
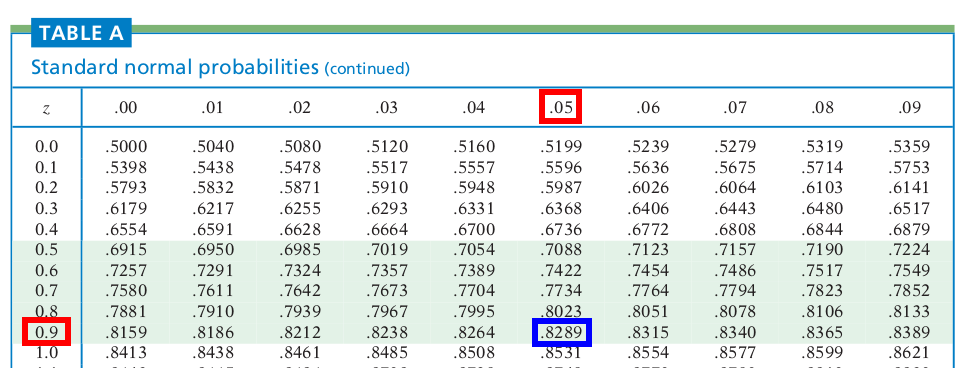
• $z<-3.4$, $P(X<x_0)\approx 0$
• $z>3.4$, $P(X<x_0)\approx 1$

Graph

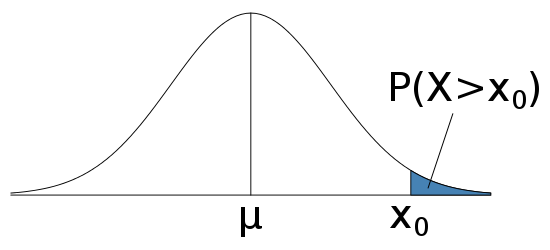
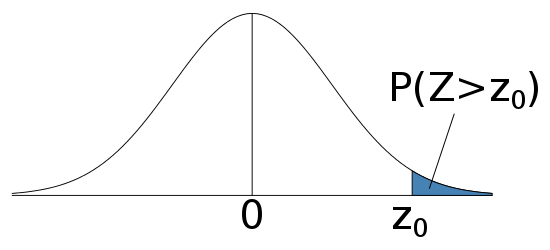
$P(X>x_0)$

• $P(X>x_0)=1-P(X<x_0)$
• Follow the previous slides to calculate $P(X<x_0)$, and then subtract that number from 1

Find $x_0$

• Look up Normal Table to find a $z$ with corresponding probability closest to $1-\alpha$%
• $x_0=z\sigma+\mu$

Sampling Distribution

• If we draw many samples from the population and calculate their mean values, then the mean also has a distribution
• If population follows Normal distribution $N(\mu, \sigma^2)$, then the mean follows $N(\mu, \sigma^2/n)$
• Sample means are less variable than individual observations
• For normal distribution, the density curve will be taller and narrower if it is less variable